l'atmosphère

L’état d’un fluide est défini par trois variables : volume (V), pression (P), température (T). La pression est uniforme dans un fluide non pesant. Dans le cas d’un gaz pesant, elle varie avec le niveau. Pour étudier les changements d’état d’une masse limitée, on peut en première approximation raisonner sur une pression moyenne uniforme régnant à l’intérieur du volume.
Les trois variables précédentes ne sont pas indépendantes. Elles sont reliées par l’équation d’état des gaz parfaits . Cette équation peut être déclinée sous différentes formes ,notamment la loi de Mariotte - Gay Lussac:

Où P est la pression en Pa

V est le volume en m3

T est la température en °Kelvin (273 + t°C)

Les gaz aérostatiques (air, hydrogène et hélium),dans les plages de température et de pression dans lesquels ils sont utilisés, peuvent être considérés comme des gaz parfaits. La présence de vapeur d’eau en faible quantité induit des corrections mineures dans les cas qui nous concernent.
Lorsque l’on mélange deux gaz à la même température, occupant initialement des volumes V₁et V₂, sous des pressions P₁et P2, la loi de Dalton s’applique alors :

Où V est le volume final

P est la pression finale

La pression dans un fluide pesant est la même en tout point d’un plan horizontal. Le principe de Pascal exprime que la différence de pression entre deux points A et B d’une même masse fluide est égale au poids d’une colonne de fluide ayant pour base l’unité de surface et pour hauteur la distance verticale entre les deux plans horizontaux passant par A et B.
Le nivellement barométrique permet d’exprimer les variations de masse volumique et de pression de l’air avec la hauteur. On peut obtenir des expressions plus ou moins complexes selon la nature des approximations retenues.

1^ère approximation : Atmosphère homogène (masse volumique constante avec l’altitude)

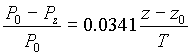
où P₀ est la pression à l’altitude de référence Z₀

P_z est la pression à l’altitude Z

T est la température moyenne entre les altitudes Z et Z₀

Cette approximation n’est admissible que pour des dénivellations inférieures à 500 m.

2^ème approximation :Loi de Halley (atmosphère isotherme)

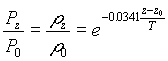
Cette approximation est admissible au-dessus de 11 000 m où la température est sensiblement constante.

3^ème approximation : Atmosphère réelle moyenne

On adopte dans ce cas une loi expérimentale de décroissance de la température avec l’altitude. On obtient alors:

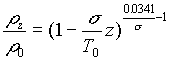
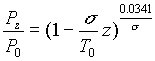
En atmosphère standard, on prend :

P₀=10330 Pa, T₀=288 °K , s = 0.0065 °K/m